重回帰分析とは
重回帰分析とは、以下の図のように複数の入力データがあり、自動的に答えを1つ求めることができます。

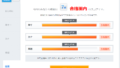
No1~No5までの土地情報があります。
| No | 駅からの距離(分) | 用途地域 | 土地価格(坪単価) |
| 1 | 6 | 第一種低層住居専用地域 | 58万 |
| 2 | 10 | 商業地域 | 60万 |
| 3 | 3 | 商業地域 | 72万 |
| 4 | 25 | 第一種低層住居専用地域 | 30万 |
| 5 | 18 | 第一種低層住居専用地域 | 40万 |
- Excelで回帰分析を行う準備は、以下のようになります。
- 用途地域は、今回、2種類のみするため、ダミー変数と呼ばれるものを設けました。男女や出欠など、数字でないものを数字に置き換えます。
- 用途地域は、1が 第一種低層住居専用地域 、0が 商業地域としました。
Excelで回帰分析
Excelでの回帰分析は、以下の手順で行います。
①メニューの[データ]の分析の中の「データ分析」を選択します。
※「データ分析」のメニューが無い場合には、アドインでインストールします。
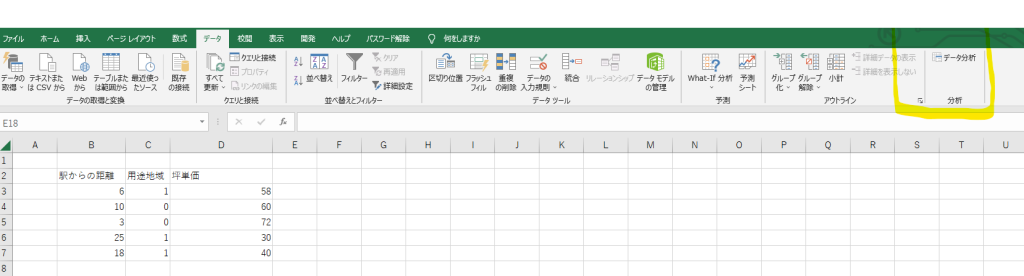
②回帰分析をクリックします。
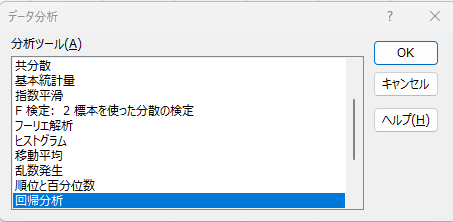
③入力Y範囲で坪単価のデータを選択します。
ラベル込みで選択すると、分析結果が見やすくなりので、ラベルにチェックします。
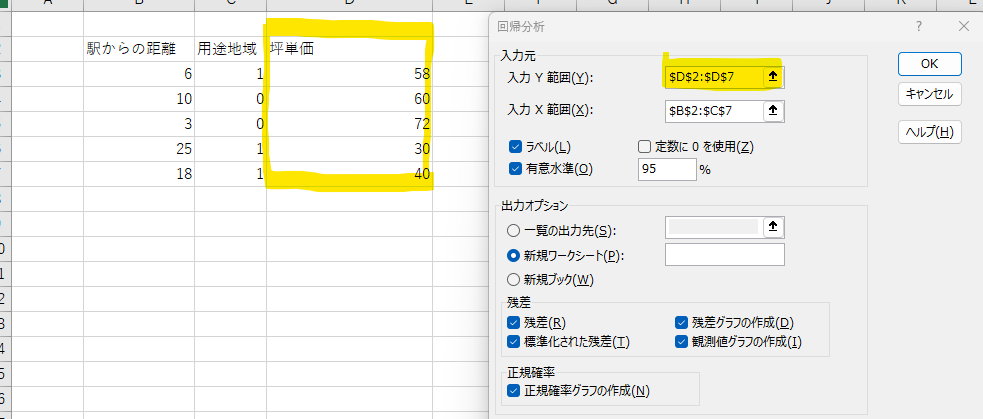
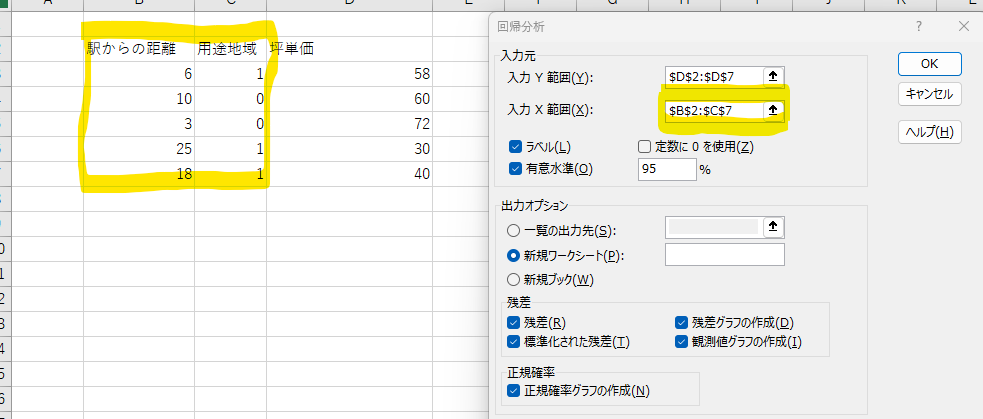
④OKボタンをクリックすると、回帰分析が終了します。
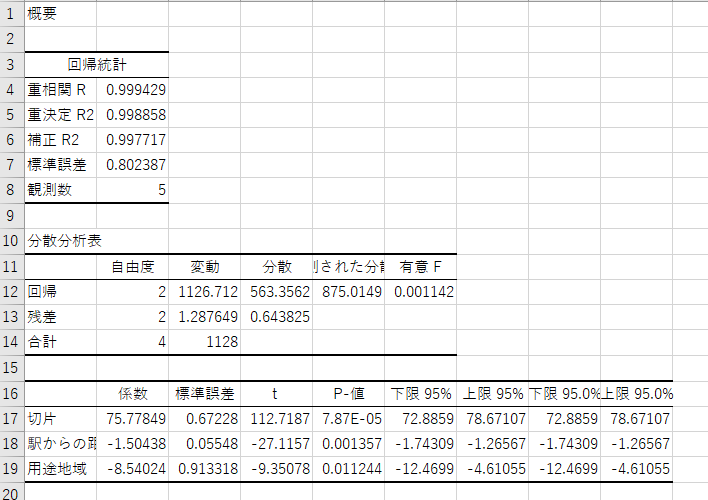
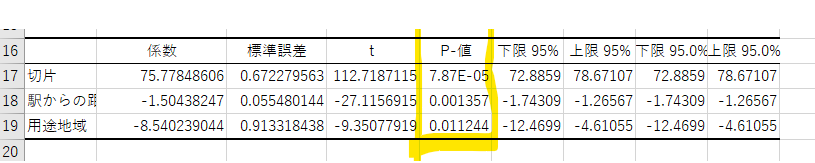
- 回帰式は、以下のようになります。
- β0(切片)、β1(駅からの距離の係数)、β2(用途地域の係数)が求まります。

上記の式に、x1「駅からの距離」、x2「用途地域」を入力すると「坪単価」が求まります。
回帰統計
以下の指標のうち、補正R2が重要です。補正R2は、1に近い程、良いモデルを表しています。
- 重相間R: 重相関係数。 実際に観測された目的変数の値と、重回帰式をあてはめて計算した推定値(理論値)との相関係数です。 1に近いほどよく近似されたモデルなります 。
- 重決定R2: 決定係数。 重相間 Rの2乗に等しい値です。
- 補正R2: 自由度修正済決定係数。 データ数が少ないと決定係数が自由度の影響を受けて実際よりも大きくなるので,自由度を考慮して補正した決定係数。この値が1に近いほど良いモデルになります。 (選択した項目が、どれだけ結果に影響を与えているか?)
- 標準誤差: 標準誤差 。
- 観測数:データ数。
寄与率
- 影響があるか判断するために、「P-値」の値を参照します。
- 一般的に0.05より小さければ「影響がある」と判断できます。