汎用補間 (距離の比による補間)
概要
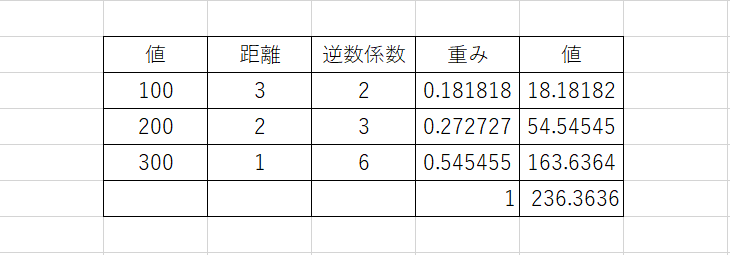
- 複数の既知の値を利用して、任意の場所の値を求めます。距離が分かれば、距離の重みで補間できます。 例えば、橙色の箇所の値は、236になります。
- 要素(3角形要素や4面体要素)は不要で、既知の点と値さえあれば補間可能です。
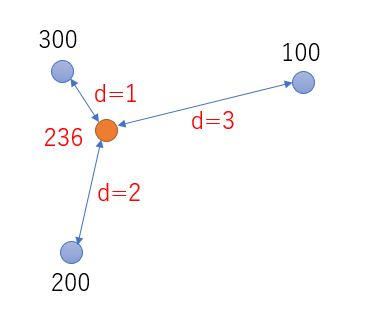
例えば100万個の座標の中から、与えられた点に最も近い点を見つけだすのは時間がかかります。 そこで、以下のようにします。
- 座標値をいくつかのエリアに分け、検索範囲をしぼる。
- 近傍点は、与えられた点に近い順に距離でソートする。
- 例えば近傍点を3個とする。3点を使用した補間を行う。。
算出式
以下の式で算出できます。
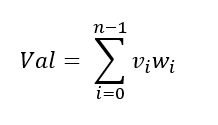
- Viは値
- Wiは重み係数です。全ての重みを足すと1.0になります。
- Wiは、以下の手順で求めることができます。
①求めたい点pとの、全ての距離を集計します。距離合計とします。
②逆数係数の算出
距離合計を各距離で割って、逆数係数を算出します。
③重み係数の算出
各逆数係数を逆数係数合計値で割ります。※重みを足すと1.0になります。
④補間値の算出
値と重み係数をかけたものを集計すると補間値が求まります。
例題
ソース
#include <iostream>
#include "Vector3D.hxx"
int main()
{
// set value
Point3D p[3];
p[0].set(3.0, 0.0, 0.0);
p[1].set(0.0, 2.0, 0.0);
p[2].set(0.0, 0.0, 1.0);
double v[3];
v[0] = 100;
v[1] = 200;
v[2] = 300;
Point3D postion(0.0, 0.0, 0.0);
// calc total distance
double totalDistance = 0.0;
for (int i = 0; i < 3; i++) {
totalDistance = totalDistance + distance(p[i], postion);
}
// calc weight
double w[3];
double wTotal = 0.0;
for (int i = 0; i < 3; i++) {
w[i] = totalDistance / distance(p[i], postion);
wTotal = wTotal + w[i];
}
for (int i = 0; i < 3; i++) {
w[i] = w[i] / wTotal;
}
// calc value
double vaule = 0.0;
for (int i = 0; i < 3; i++) {
vaule = vaule + v[i] * w[i];
}
std::cout << "vaule = " << vaule << std::endl;
return 0;
}
直線補間
概要
- 2点間の値は、距離に応じて補間できます。
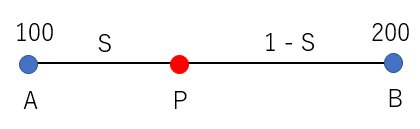
算出式
- A,Bは各点の値
- Sは、線分の距離を1とした時の割合
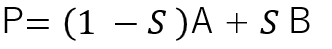
例題
- 各点の値を100,200とした場合、中点の値は150。
ソース
#include <iostream>
#include "Vector3D.hxx"
int main()
{
// set value
Point3D At(0.0, 0.0, 0.0);
Point3D Bt(100.0, 0.0, 0.0);
Point3D Pt(50.0, 0.0, 0.0);
double A = 100.0;
double B = 200.0;
//calc value
double S = distance(At,Pt) / distance(At, Bt);
double P = ( 1 - S ) * A + S * B;
std::cout << "value = " << P << std::endl;
return 0;
}3角形の補間
概要
- 3角形の各点の値が既知の場合、内部の任意点の値が取得できます。
- 面積座標(重心座標)を利用して、値を求めることができます。
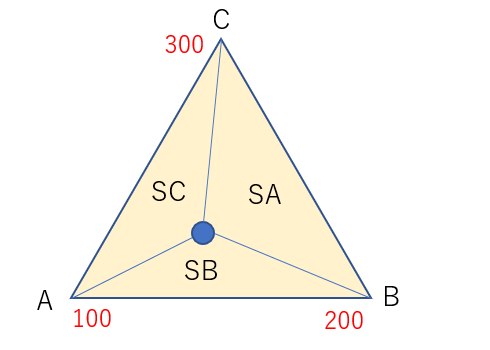
- 任意点が3角形上に存在しない場合、任意点を3角形に射影したりして、面上に乗っかるようにします。
算出式
以下の式で、算出できます。
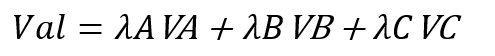
- λA~ λCは、SA~SCの面積比。1=λA+λB+λC とした場合の面積比です。
- VA~VCは、節点値です。
例題
節点値がそれぞれ100,200,300の場合、重心点の値は200となります。
ソース
#include <iostream>
#include "Vector3D.hxx"
int main()
{
// set value
Point3D A(0.0, 0.0, 0.0);
Point3D B(100.0, 0.0, 0.0);
Point3D C(100.0, 100.0, 0.0);
double VA = 100.0;
double VB = 200.0;
double VC = 300.0;
// set center of triangle
Point3D postion(200.0/3.0, 100.0/3.0, 0.0);
//calc value
double area = crossProduct(C - A, B - A).norm() * 0.5;
double rA = ( crossProduct(B - postion, C - postion).norm() * 0.5 ) / area;
double rB = ( crossProduct(C - postion, A - postion).norm() * 0.5 ) / area;
double rC = ( crossProduct(A - postion, B - postion).norm() * 0.5 ) / area;
double value = rA * VA + rB * VB + rC * VC;
std::cout << "value = " << value << std::endl;
return 0;
}
4面体の補間
概要
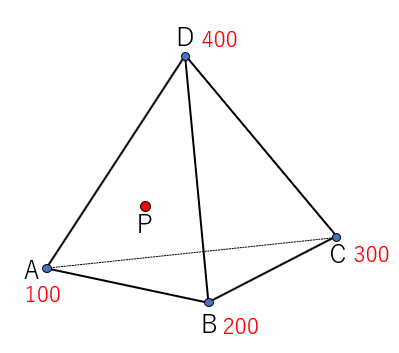
- 4角形の各点の値が既知の場合、内部の任意点の値が取得できます。
- 体積比を利用して、値を求めることができます。
算出式
- 以下の式で、算出できます。
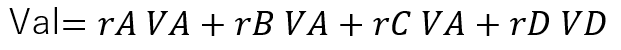
- rA ~ rD は、 点Pと各面とで作られる4面体の体積比。
- 節点Pと接続する要素は、C, B, D, PとB, A, D, PとA, C, D, PとC, A, B, Pです。
- 体積計算時、要素を構成する点の並びを変えるとマイナスの体積なるの留意が必要です。(例えば C、 B、 D、 P ⇒ B、C、D、Pとした場合 など)
- 体積比は、1=rA+rB+rC+rD とした場合の体積比です。
- VA~VDは、各節点値です。
例題
- 節点値が、100,200,300,400の場合、重心点の値は250になります。
ソース
#include <iostream>
#include "Vector3D.hxx"
double GetTetVolume(const Point3D& v1, const Point3D& v2, const Point3D& v3, const Point3D& v4)
{
double value =
( (v2.x() - v1.x()) * ((v3.y() - v1.y()) * (v4.z() - v1.z()) - (v4.y() - v1.y()) * (v3.z() - v1.z()))
- (v2.y() - v1.y()) * ((v3.x() - v1.x()) * (v4.z() - v1.z()) - (v4.x() - v1.x()) * (v3.z() - v1.z()))
+ (v2.z() - v1.z()) * ((v3.x() - v1.x()) * (v4.y() - v1.y()) - (v4.x() - v1.x()) * (v3.y() - v1.y()))
) / 6.0;
return value;
}
int main()
{
// set value
Point3D A(0.0, 0.0, 0.0);
Point3D B(100.0, 0.0, 0.0);
Point3D C(100.0, 100.0, 0.0);
Point3D D(100.0, 100.0, 100.0);
double VA = 100.0;
double VB = 200.0;
double VC = 300.0;
double VD = 400.0;
Point3D P(300.0/4.0, 200.0/4.0, 100.0/4.0);
//calc value
double volume = GetTetVolume(A, B, C, D);
double rA = abs( GetTetVolume(C, B, D, P) / volume );
double rB = abs( GetTetVolume(B, A, D, P) / volume );
double rC = abs( GetTetVolume(A, C, D, P) / volume );
double rD = abs( GetTetVolume(C, A, B, P) / volume );
double value = rA * VA + rB * VB + rC * VC + rD * VD;
std::cout << "value = " << value << std::endl;
return 0;
}

